02b: Algorithms: Big-O

ICS211, Spring 2013
Dr. Zach

(switch view)

Status

Comparing Algorithms

Comparing Implementations

Benchmarking is still useful when comparing two implementations in very specific contexts. But those measurements don't let you compare algorithms, nor are they useful in different contexts (hardware, language, etc.).

Comparing Algorithms: Number of steps involved?

Comparing Algorithms: upper-bound of growth rate!

Example (variant of p.81)

for (int k = 0; k < n; k++) {
  //statement 1
  //statement 2
  //...
  //statement 5
}
//...25 more statements...
for (int i = 0; i < n; i++) {
  for (int j = 0; j < n; j++) {
    //statement 1
    //statement 2
  }
}

Time to run = T(n) = n*5 + 25 + n*n*2 = 2n2 + 5n + 25
(assuming each statement takes 1 "tick" to run)

Big-O Defined

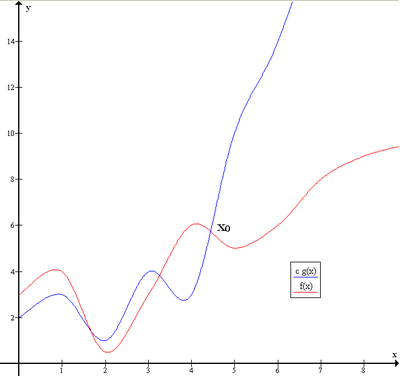
Graph of f(n) and g(n), which correspond to T(n) and f(n) in the definition given here.

Here, I defined Big-O for T(n) in terms of f(n). In other contexts, you'll see the big-O of any function f(n) defined in terms of g(n). Same thing. Just replace f(n) with g(n) above, and then T(n) with f(n). You end up with:

f(n) = O(g(n)) as n->∞ iff ...(etc)...

which is the definition format you'll often see in other sources.

Big-O Definition Example

(Note we could have selected f(n) = 8n2 + n OR f(n) = n4 here instead. Valid, but convention (especially in this class) is to choose the simplest and lowest-order f(n) that you can.)

Big-O Definition Revisited

Informal Approach

Summary: Big-O tells us the algorithm won't grow any faster (get any worse) than a given f(n), no matter how many more processed elements are added.

Big-O Example: Search (p.78)

/** Returns index of target found in x array, or -1 if not found */
public static int search(int[] x, int target) {
  for (int i = 0; i < x.length; i++) {
    if (x[i] == target) {
      return i;
    }
  }
  return -1;  //looped through whole array and didn't find target
}

Big-O Example: Back and Forth

/** Prints the given array forward and then backwards. */
public static void backAndForth(int[] nums) {
  //forward
  for (int n : nums) {
    System.out.print(n);
    System.out.print(" ");
  }
  System.out.println();

  //backwards
  for (int i = nums.length - 1; i >= 0; i--) {
    System.out.print(nums[i]);
    System.out.print(" ");
  }
  System.out.println();
}

Big-O Example: Box

/** Prints a box of #s of width * height.  */
public static void drawBox(int width, int height) {
  for (int row = 0; row < height; row++) {
    for (int col = 0; col < width; col++) {
      System.out.print('#');
    }
    System.out.println();
  }
}

Big-O Example: Many boxes

/** Prints 5 boxes of the given size.  */
public static void drawBoxes(int size) {
  for (int i = 0; i < 5; i++) {
    drawBox(size, size);
    System.out.println();
  }
}

Big-O Example: Many boxes variant

/** Prints the given number of boxes.  */
public static void drawBoxes(int many) {
  for (int i = 0; i < many; i++) {
    drawBox(10, 10);
    System.out.println();
  }
}

Big-O Example: Find duplicates

/** Returns whether there are any repeated values in the given array. */
public static boolean findDuplicates(int[] nums) {
  for (int i = 0; i < nums.length; i++) {
    for (int j = i + 1; j < nums.length; j++) {
      if (nums[i] == nums[j]) {
        return true;
      }
    }
  }
  return false;
}

Lessons from Examples

Some Big-O Limitations: vs reality

Java Review

Arrays and reading from a file

Arrays

int[] nums = {5, 6, 90};
int[] ages = new int[10];
int size = nums.length;

nums[1] = 60;
for (int i = 0; i < nums.length; i++) {  //use .length, not 3 here
  nums[i]++;
}
for (int n : nums) {
  System.out.println(n);
}

Again, review: should already know this.

Arrays of Arrays (Multi-dimensional)

char[][] ticTacToe = new char[3][3];
tictactoe[1][1] = 'X';
char[] middleRow = ticTacToe[1];
System.out.println(middleRow[1]);

int[][] matrix = new int[4][];  //sub-arrays can be different size if created later
for (int i = 0; i < matrix.length; i++) {
  matrix[i] = new int[i + 1];
}
matrix[1][1] = 9;

Command Line Arguments

public class Hello {
  public static void main(String[] args) {
    //...
  }
}

Cmd line args examples


Reading from a file

import java.util.Scanner;
import java.io.File;
import java.io.IOException;

public class PrintFile {
  /** Prints to the screen the contents of the file named input.txt. */
  public static void main(String[] args) {
    try {
      Scanner file = new Scanner(new File("input.txt"));
      while (file.hasNextLine()) {
        String line = file.nextLine();
        System.out.println(line);
      }
      file.close();
    }catch (IOException e) {
      System.out.println("Could not read from file: " + e.getMessage());
    }
  }
}

Reading from a file details

Reading from a file: Alternative

import java.io.IOException;
import java.io.FileReader;
import java.io.BufferedReader;

public class Hello {
  /** Prints to the screen the contents of the file named input.txt. */
  public static void main(String[] args) {
    try {
      BufferedReader file = new BufferedReader(new FileReader("input.txt"));
      String line = file.readLine();
      while (line != null) {
        System.out.println(line);
        line = file.readLine();
      }
    }catch (IOException e) {
      System.out.println("Could not read from file: " + e.getMessage());
    }
  }
}

Interesting aside

String line = file.readLine();  //initializer
while (line != null) {          //condition
  System.out.println(line);
  line = file.readLine();       //"increment"
}

Those are the components of a for loop... 

for (String line = file.readLine(); line != null; line = file.readLine()) {
  System.out.println(line);
}

Could have done something similar with a Scanner too (tho not quite as gracefully): 

for (String line = null; file.hasNextLine(); line = file.nextLine()) {
  if (line != null) {
    System.out.println(line);
  }
}

Summary

For next time...